Теоремы тригонометрия
Список теорем:
- Теорема Стогова "о синусах"
- Теорема Стогова "о числах золотого сечения"
- Теорема Стогова "о способах выражения линейных размеров в угловые и обратно".
- Теорема Стогова "о признаках делимости значений прогрессии"
- Теорема Стогова "о разрядности длины окружности равной 1 градусу".
- Теорема Стогова "О длине эллипса".
1. Теорема Стогова "о синусах"
Синус это коэффициент пропорциональности длины хорды окружности к ее диаметру. Хорда образует угол внутри окружности, равно как и угол образует хорду на окружности. Синус это значение, показывающее во сколько раз хорда меньше диаметра и определяется как отношение длины хорды к диаметру. Не имеет значения как сказать "синус угла" или "синус хорды", потому что каждому углу соответствует своя хорда на окружности. Объяснить суть термина синус без привлечения окружности можно только для прямоугольного треугольника, потому что его гипотенуза совпадает с диаметром окружности.
Например если мы возьмем синус 90 градусов мы видим, что хорда совпадает с диаметром, поэтому коэффициент пропорциональности (Sin) между диаметром и хордой будет равен 1.
На картинке показан пример расчета (Sin) для произвольного угла.
Таким образом по углу мы можем найти хорду, равно как и по хорде определить угол.
Следовательно мы имеем расчетную логику, при которой значение синуса угла будет определяться как отношение хорды окружности к ее диаметру и следовательно угла, который образует хорда.
Очевидно, что значение синуса хорды (угла) существует только в пределах от 0 до 90 градусов для каждой четверти окружности и в значениях от -1 до 1. Следовательно все расчетные значения синусов это 4 ряда (квадранта) повторяющихся значений соответствующие каждой четверти окружности.
Например:
1 четверть окружности
sin(1°) = 0,01745240644
2 четверть окружности
sin(179°) = 0,01745240644
3 четверть окружности
sin(181°) = -0,01745240644
4 четверть окружности
sin(359°) = -0,01745240644
Для нашего примера на картинке:
1 четверть окружности
sin(64°) = 0,8988
2 четверть окружности
sin(116°) = 0,8988
3 четверть окружности
sin(244°) = -0,8988
4 четверть окружности
sin(296°) = -0,8988
Следовательно имеем расчетную логику:
Так как значение синуса это отношение постоянно уменьшающейся хорды окружности к ее диаметру, имеем отношение, где числителем будет постоянно уменьшающийся диаметр, а знаменателем будет сам диаметр. Именно таким образом была составлена Таблица Брадиса.
2. Теорема Стогова "о числах золотого сечения"
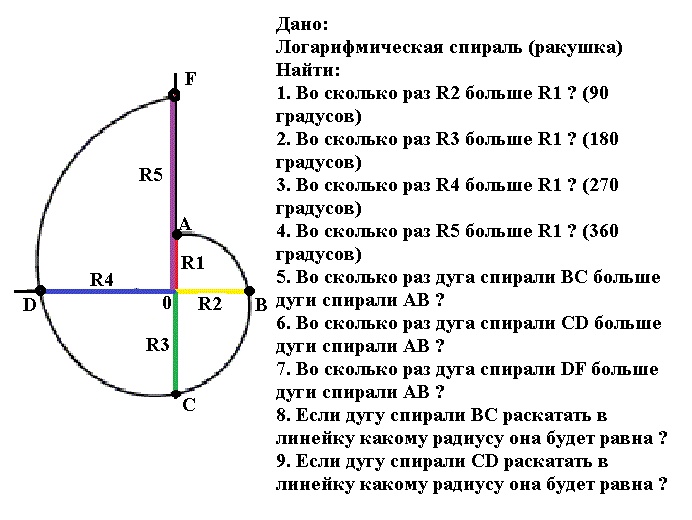
Золотое сечение это пропорция увеличения радиуса золотой (логарифмической) спирали на определенное количество градусов спирали.
Вопрос бота: Как были вычислены значения которые называют "Ряд Фибоначчи или "ряд Пизанского".
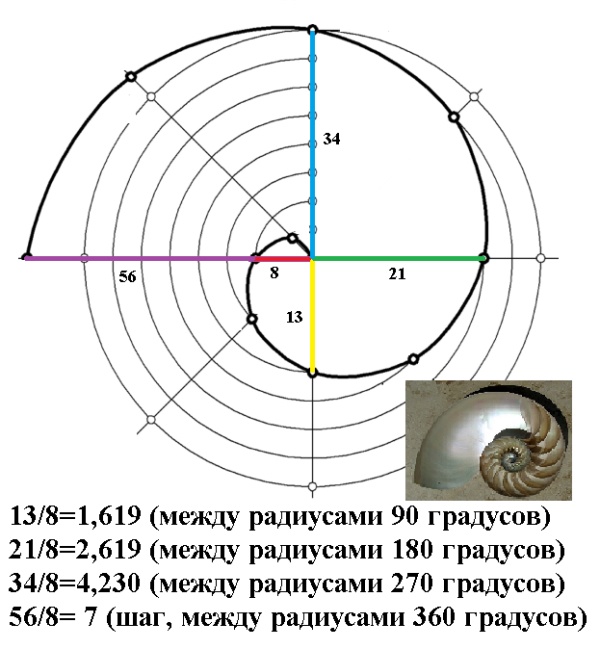
Ответ чела: Взяли простую раковину и измерили ее радиусы через каждые 90 градусов получили значения: 3,5,8,13,21,34,55,89 и так далее. Отношение двух радиусов между которыми 90 градусов, например 13 и 8, поделили их и получили "число золотого сечения" равное 1,62.
Если мы возьмем два радиуса между которыми 180 градусов получим "число золотого сечения" 2,6.
Если возьмем 270 градусов то получим "число золотого сечения" равное 4,3.
Если возьмем 360 градусов мы получим "число золотого сечения" равное 7 (семи).
Т.е. само число не является универсальным значением, универсальным является коэффициент пропорции в который увеличивается радиус золотой спирали на определенное количество градусов. Таким образом значения ряда Пизанского (Фибоначчи) не площади как Вам рассказывали в школе, но постоянно увеличивающиеся радиусы золотой спирали.
Конфигурация:
Между радиусами 90° число золотого сечения равно 13/8 = 1,6
Между радиусами 180° число золотого сечения равно 21/8 = 2,6
Между радиусами 270° число золотого сечения равно 34/8 = 4,3
Между радиусами 360° число золотого сечения равно 56/8 = 7
Где +7 главный коэффициент, показывающий во сколько раз увеличивается радиус целого витка золотой спирали, где 1,62 лишь частный случай, коэффициент, показывающий во сколько раз увеличивается радиус спирали на каждые 90 градусов.
На каждые 90 градусов радиус золотой спирали увеличивается в 1,62 раза
На каждые 180 градусов радиус золотой спирали увеличивается в 2,6 раза
На каждые 270 градусов радиус золотой спирали увеличивается в 4,3 раза
На каждые 360 градусов радиус золотой спирали увеличивается в 7 раз
Во сколько раз увеличивается радиус золотой спирали на 1 градус ???
7/360 = 0,01944 ??
Следи.
Если мы замкнутую окружность в 360 градусов раскатаем в линейку, то длина этой линейки будет в 3,1415 (Пи) раз длиннее чем диаметр окружности, а расстояние радиуса на линейке в 57,2958° будет равно 1 РАдиану.
360 / 2 / 3,1415 = 57,2958°
Следовательно в замкнутой окружности вмещается: 360/57,2958 = 6,283 РА.
Т.е. 6 целых дуг по 57,2958° и 0,28 седьмой дуги. Для того, чтобы в окружности вместилось ровно 7 РАдиусов, ее необходимо разорвать в золотую спираль, в которой радиус будет расти в ,,,,,,,, раз на каждый градус витка спирали в которой 360 градусов. И только в этом случае в один виток золотой спирали "влезет" ровно 7 дуг по 1 РАдиану. Что и требовалось доказать.
Дано:
Длина всей окружности длиннее чем ее диаметр в Пи раз (3,1415)
Длина всей окружности длиннее чем ее радиус в 2Пи раз (6,28)
Длина окружности равная ее радиусу (1 Радиан) равно:
Количество градусов на шкале/Пи/2 (Например 360/Пи/2=57,2957°, или для примера 365/Пи/2=58,091°)
Длина окружности равная ее диаметру (2 Радиана) равно: Количество градусов на шкале/Пи (Например 360/Пи=114,591°, или для примера 365/Пи=116,1831°)
Например есть окружность диаметром 10 см.
Длина всей окружности равна 10*3,14=31,4 см.
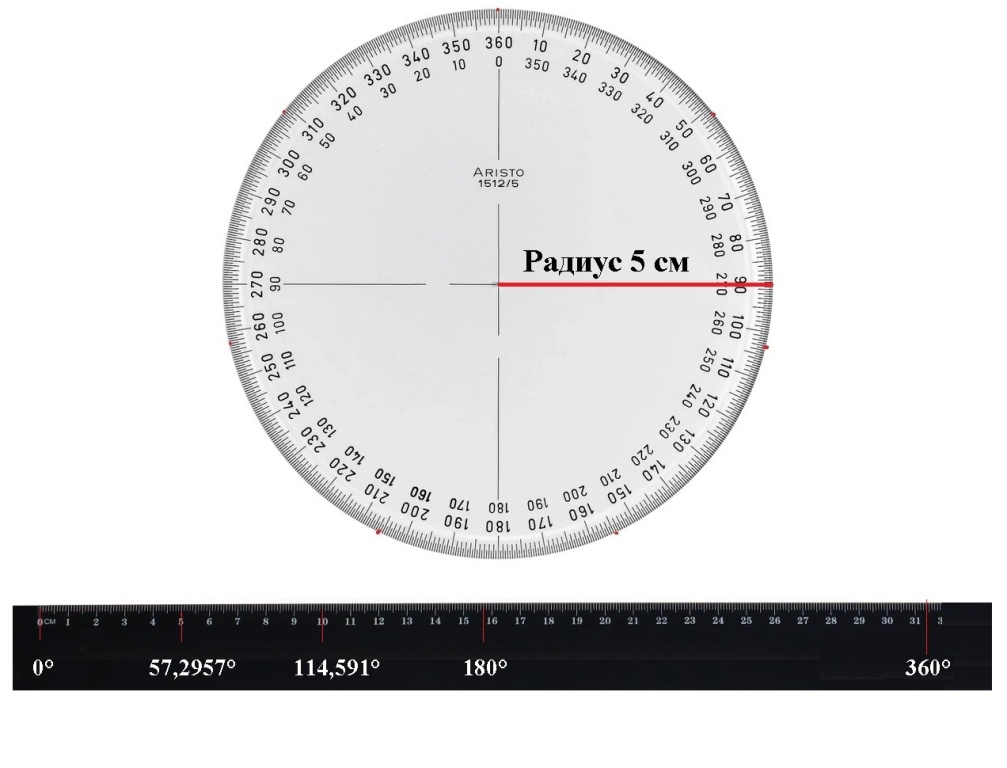
На прямой линейке мы имеем расстояния:
5 см - радиус - 1 радиан (57,2957°),
10 см - диаметр - 2 радиана (114,591°),
15,7 см это 180° окружности и т.д.
Таким образом линейные размеры можно выразить в угловых, т.е. градусы перевести в сантиметры, метры или километры. Если мы окружность с диаметром 10 см выгнем в прямой отрезок он будет больше диаметра в Пи раз, т.е. = 31,4 см.
Докажем теорему:
Дано:
Диаметр окружности 10 см
Радиус окружности 5 см
Длина всей окружности D*Пи =31,4 см (360 градусов)
Имеем пропорцию 31,4 см = 360 градусов
Разместим на линейке в 31,4 см 360 градусов путем расчетной логики:
1 см линейки = 360/31,4 = 11,464°
0,1 см линейки 11,464°/10 = 1,146°
0,01 см линейки = 11,464°/100 = 0,1146°
0,001 см линейки = 11,464°/1000 = 0,011°
...
0,2 см линейки = 1,146°*2 = 2,292°
0,3 см линейки = 1,146°*3 = 3,439°
...
5 см линейки (радиус) = 1,146°*50 = 57,324° (1 радиан)
...
10 см линейки (диаметр) = 1,146°*100 = 114,649°(2 радиана)
...
15,7 см линейки = 1,146°*157 = 180°
...
31,4 см линейки = 1,146°*314 = 360°
Таким образом линейные размеры могут выражаться в угловых, равно как и наоборот, что и требовалось доказать.
4. Теорема Стогова "о признаках делимости значений прогрессии"
1. Если признак делимости выполняется для числа, он выполняется и для любого числа его геометрической (двоичной) и кубической прогрессии.
Например:
Признак делимости на 4 : число делится на 4, если оканчивается на 00, или число, составленное из ДВУХ последних цифр данного числа, делится на 4. Примеры: а) 78 536 делится на 4, так как 36 делится на 4; б) 8422 не делится на 4, так как 22 не делится на 4.
Увеличиваем геометрическую прогрессию числа 4 до 8...
Признак делимости на 8 : число делится на 8, если оканчивается на 000, или число, составленное из ТРЕХ последних цифр данного числа, делится на 8. Примеры: а) 78 536 делится на 8, так как 536 делится на 8; б) 89422 не делится на 8, так как 422 не делится на 8.
Увеличиваем геометрическую прогрессию числа 4 до 16...
Признак делимости на 16 : число делится на 16, если оканчивается на 0000, или число, составленное из ЧЕТЫРЕХ последних цифр данного числа, делится на 16. Примеры: а )78 192 делится на 16, так как 192 делится на 16; б) 898422 не делится на 16, так как 422 не делится на 16....
Следовательно мы имеем расчетную логику для любого числа возвышенного в геометрической прогрессии числа 4. Таким образом признак делимости на 4 выполняется ко всем числам геометрической прогрессии числа 4...
То же самое для "признака делимости на число 3"
То же самое для "признака делимости на число 5"
То же самое для "признака делимости на число 8"
То же самое для "признака делимости на число 9"
Следовательно если выполняется признак делимости на число, он выполняется и для любого числа его геометрической прогрессии.
2. Основные виды прогрессий (степенных рядов)
Двоичная (геометрическая) прогрессия, когда значения постоянно умножаются на 2.
Числа 2,4 и 8 числа одной двоичной (геометрической) прогрессии вида 2,4,8,16,32...
Числа 3,6 числа одной двоичной (геометрической) прогрессии вида 3,6,12,24,48...
Число 5 имеет двоичную прогрессию вида 5,10,20,40,80...
Число 7 имеет двоичную прогрессию вида 7,14,28,56,112,224,448...
Число 9 имеет двоичную прогрессию вида 9,18,36,72,144,288,576...
Кубическая прогрессия, когда значения постоянно увеличиваются в 3 раза.
Число 2 имеет кубическую прогрессию вида 2,6,18,54,162,486,1458...
Число 3 имеет кубическую прогрессию вида 3,9,27,81,243,729...
Число 4 имеет кубическую прогрессию вида 4,12,36,108,324,972...
Число 5 имеет кубическую прогрессию вида 5,15,45,135,405,1215...
Число 6 имеет кубическую прогрессию вида 6,18,54,162,486,1458..
Видно, что числа 2 и 6 числа одной кубической прогрессии.
Число 7 имеет кубическую прогрессию вида 7,21,63,189,567
Число 8 имеет кубическую прогрессию вида 8,24,72,216,648,1 944
Число 9 имеет кубическую прогрессию вида 9,27,81,243,729,2187
Видно, что числа 3 и 9 числа одной кубической прогрессии.
Квадратурная прогрессия частный случай двоичной прогрессии с пропуском одного значения (витка), например
Число 2 имеет квадратурную прогрессию вида 2,8,32,128,512,2048 (значений 4,16,64 нет, которые есть на двоичной)
Следовательно если признак делимости выполняется для числа, он выполняется и для любого числа его геометрической (двоичной) и кубической прогрессии, что и требовалось доказать.
5. Теорема Стогова "о разрядности длины окружности равной 1 градусу".
Дано:
Если мы окружность выгнем в прямой отрезок он будет в Пи раз длиннее чем диаметр окружности.
Следовательно мы имеем расчетную логику:
Длина всей окружности длиннее чем ее диаметр в Пи раз (3,1415)
Длина всей окружности длиннее чем ее радиус в 2Пи раз (6,28)
Длина окружности равная ее радиусу (1 Радиан) равно: Количество градусов на шкале/Пи/2 (Например 360/Пи/2=57,2957, или 365/Пи/2=58,091)
Длина окружности равная ее диаметру (2 Радиана) равно: Количество градусов на шкале/Пи (Например 360/Пи=114,591, или 365/Пи=116,1831)
Длина целой окружности длиннее ее диаметра в Пи раз (3,14) (текущее)
Длина 1/2 окружности длиннее ее диаметра в Пи/2 раз (1,57)
Длина 1/4 окружности длиннее ее диаметра в Пи/4 раз (0,785)
Длина 1/8 окружности длиннее ее диаметра в Пи/8 раз (0,392)
Длина 1/16 окружности длиннее ее диаметра в Пи/16 раз (0,196)
Длина 1/32 окружности длиннее ее диаметра в Пи/32 раз (0,098)
Длина 1/64 окружности длиннее ее диаметра в Пи/64 раз (0,0490)
Длина 1/128 окружности длиннее ее диаметра в Пи/128 раз (0,0245)
Длина 1/256 окружности длиннее ее диаметра в Пи/256 раз (0,012)
Длина 1/512 окружности длиннее ее диаметра в Пи/512 раз (0,0061359)
Длина 1/1024 окружности длиннее ее диаметра в Пи/1024 раз (0,003067)
......
Длина 1/6,33825E+29 окружности длиннее ее диаметра в Пи/633825300114115000000000000000 раз (0) (Граница)
Мы видим, что разрядность не можем увеличиваться бесконечно, но вырождается ли в ноль ?
Таким образом число Пи не константа, не является "иррациональным числом", но является текущим значением, показывающим во сколько раз длина окружности или ее дуги больше ее диаметра.
Таким образом число Пи равное 3,1415 это значение показывающее отношение ВСЕЙ длины окружности к ее диаметру.
Например:
Число Пи для всей длины окружности равно 3,14
Число Пи для половины окружности равно 1,57
Число Пи для...
Данная расчетная логика справедлива для любого количества градусов которое мы выберем, например 360, 356 или 520, а не только для 360.
Допустим мы остановимся на значении Пи/1024, тогда получаем 3,141592/1024=0,003067
Таким образом выбрав разрядность 1024 получим длину окружности в 1 градус равную 0,003067 у.е.
Теперь когда мы знаем длину 1 градуса, мы можем выбрать количество градусов в окружности.
Например 360 градусов 32 разряда длина окружности 1 градуса 0,098, что и требовалось доказать.
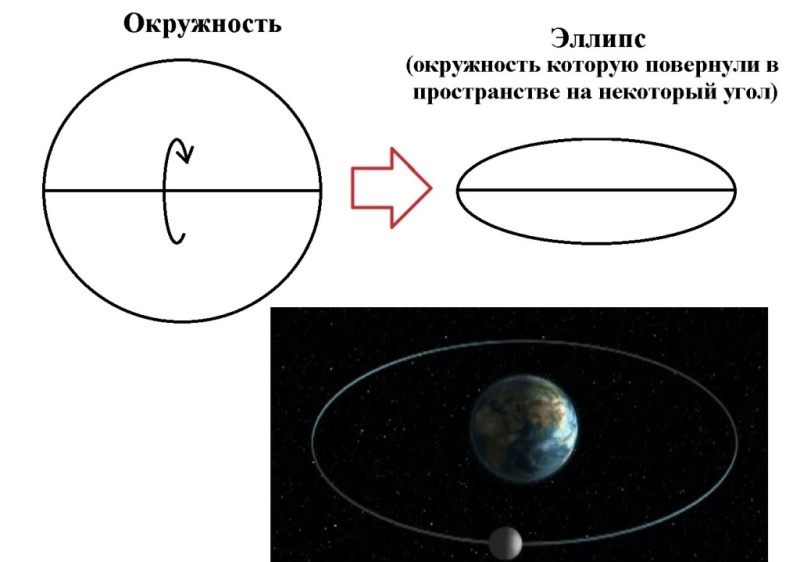
6. Теорема Стогова "О длине эллипса"
Эллипс это геометрическая фигура имеющая два диаметра - Большой (большая полуось) и малый (малая полуось). Произведение среднеарифметического двух диаметров на число Пи будет являться длиной эллипса. (2R1+2R2) / 2*Пи
Длина эллипса (6+14)/2*Пи=31,4 см
(2*3+2*7)/2*3,14=31,4 см
Формула длины окружности 2ПR, все радиусы окружности равны. Для расчета длины эллипса мы берем самый большой радиус и самый малый радиус вычисляем его среднепропорциональное (среднеарифметическое) и дополняем формулу окружности.
В результате длина эллипса равна (2R1+2R2) / 2*Пи, где (2R1+2R2) / 2 по сути является формулой 2R для вычисления длины окружности. Вы же не станете утверждать что средний радиус для эллипса не является эквивалентом постоянного радиуса для окружности..
--------------------------------------------------------------------------------
Окружность — это замкнутая плоская кривая, все точки которой равноудалены от одной неподвижной точки — центра окружности. Никакая длина окружности не может быть прямой линией, но всегда ломанной, поэтому окружность это всегда многоугольник число углов которого определяет степень совершенства самой окружности. Невозможно провести прямую линию через две хорды окружности. Начало формирования окружности треугольник - первый многоугольник с тремя углами. Увеличивая число углов мы приближаем геометрию многоугольника к геометрии окружности и на каком то определенном количестве углов наш глаз перестанет замечать сами углы и станет воспринимать многоугольник как идеальную окружность. Если невозможно провести прямую через две хорды окружности то и сама окружность является многоугольником ???
Математика это инструмент выражения сути природных явлений и физических процессов в форме символов и знаков, а также выражение зависимостей одних процессов от других в формульном виде.
Прогрессия суть последовательность чисел получаемых только умножением, а число на которое умножается другое число называют "знаменатель", но знаменатель всегда деление и результат деления. Думаю более правильно его называть числитель
Слово «сфера» происходит от древнегреческого слова ««σφαῖρα» (sphaîra), что означает «мяч, шар, ядро». » (sphaira), которое означает «шар». Сфера не поверхность шара, сфера это и есть шар.
Синус 90 градусов равен 1
Синус 30 градусов равен 0,5
угол уменьшен в 3 раза (90/3) а значение синуса уменьшено в 2 раза (1/2)
угол уменьшен в 2 раза (90/2) значение синуса уменьшилось в 1,414213562546190097624563708204 раза, а Sin 45° составляет ровно половину от значения в которое уменьшено значение синуса. 1,414213562546190097624563708204/2= Sin45°=0,707106781273095048812281854102, следовательно мы имеет расчетную логику, при которой уменьшая угол в N мы будем иметь значение синуса уменьшенное в Z раз и само значение синуса путем деления на 2.